TwoDG.jl brings together three finite element discretization schemes in a Julia package, enabling researchers to solve challenging PDEs with high-order accuracy, from wave scattering to compressible flows with shocks. I wrote TwoDG.jl from scratch as part of the MIT class 16.930: Advanced Topics in Numerical Methods for Partial Differential Equations. In this class helper functions were provided in Python and MATLAB, but I decided that it would be fun to rewrite it in Julia!
Figure 1. Compressible flow through a channel with a bump, showing the evolution of Mach number. Computed using Discontinuous Galerkin method with 5th-order polynomials and explicit Runge-Kutta time integration on the 2D Euler equations.
When you drive your car fast enough through a tunnel, the air flowing around it creates complex pressure patterns and shock waves. These same phenomena occur in jet engines, rocket nozzles, and supersonic aircraft. In the animation above, you can see a simulation of compressible gas flowing through a channel with a 0.2-unit bump at the bottom. The color represents the Mach number—how fast the fluid is moving relative to the speed of sound. Notice how the flow accelerates (turns red) as it passes over the bump, and how disturbances propagate both upstream and downstream as waves. When the flow encounters the bump, it creates shock waves and complex wave patterns that are notoriously difficult to compute accurately.
Below I show two more examples of solutions to partial differential equations (PDEs) with pretty pictures:
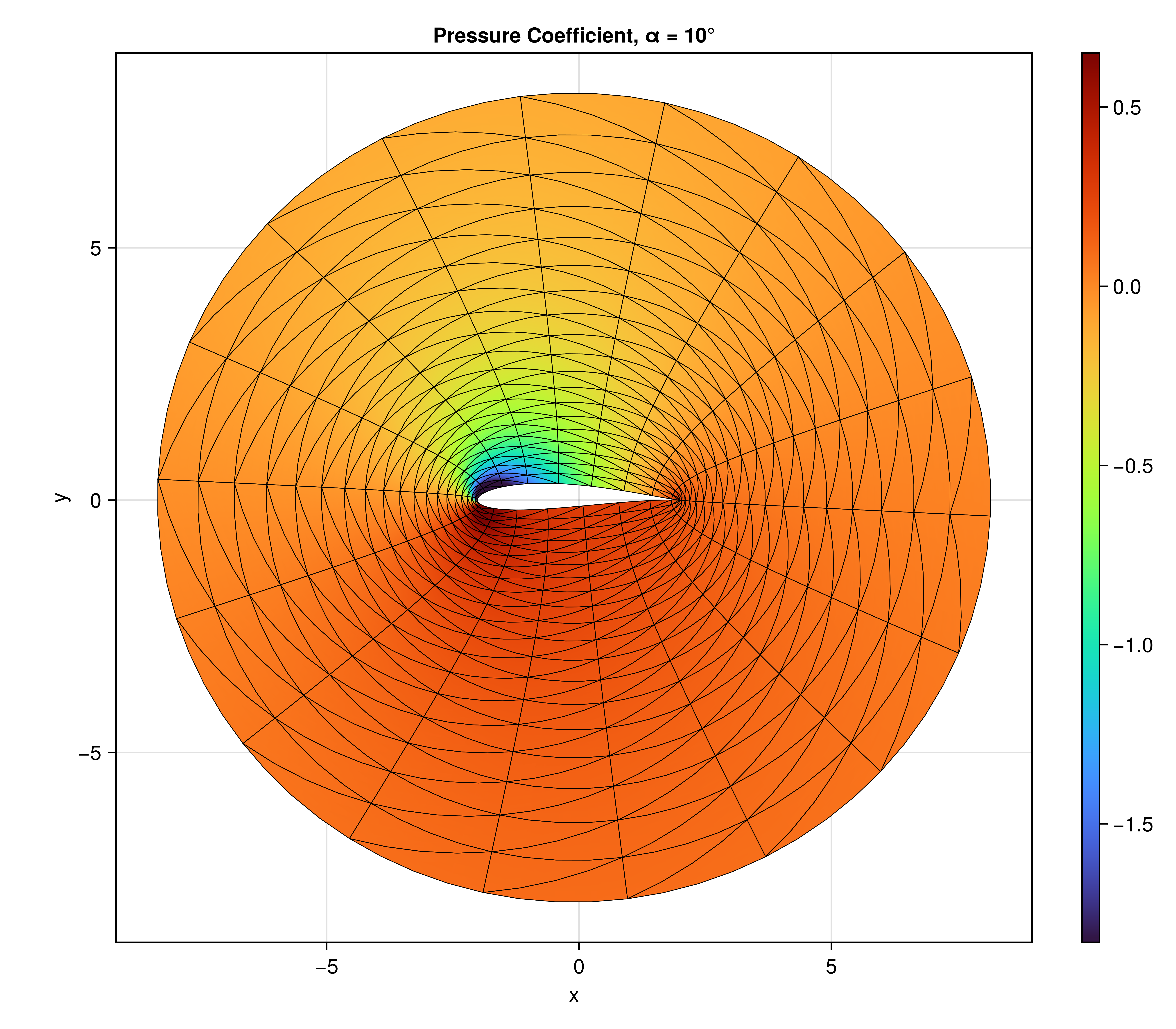Figure 2. Pressure coefficient distribution for potential flow around a circular domain computed on a Trefftz airfoil. Colors indicate pressure relative to freestream conditions, with high pressure (stagnation) below the airfoil and lower pressure above, generating lift. The angle of attack α affects the amount of lift that is able to be generated.
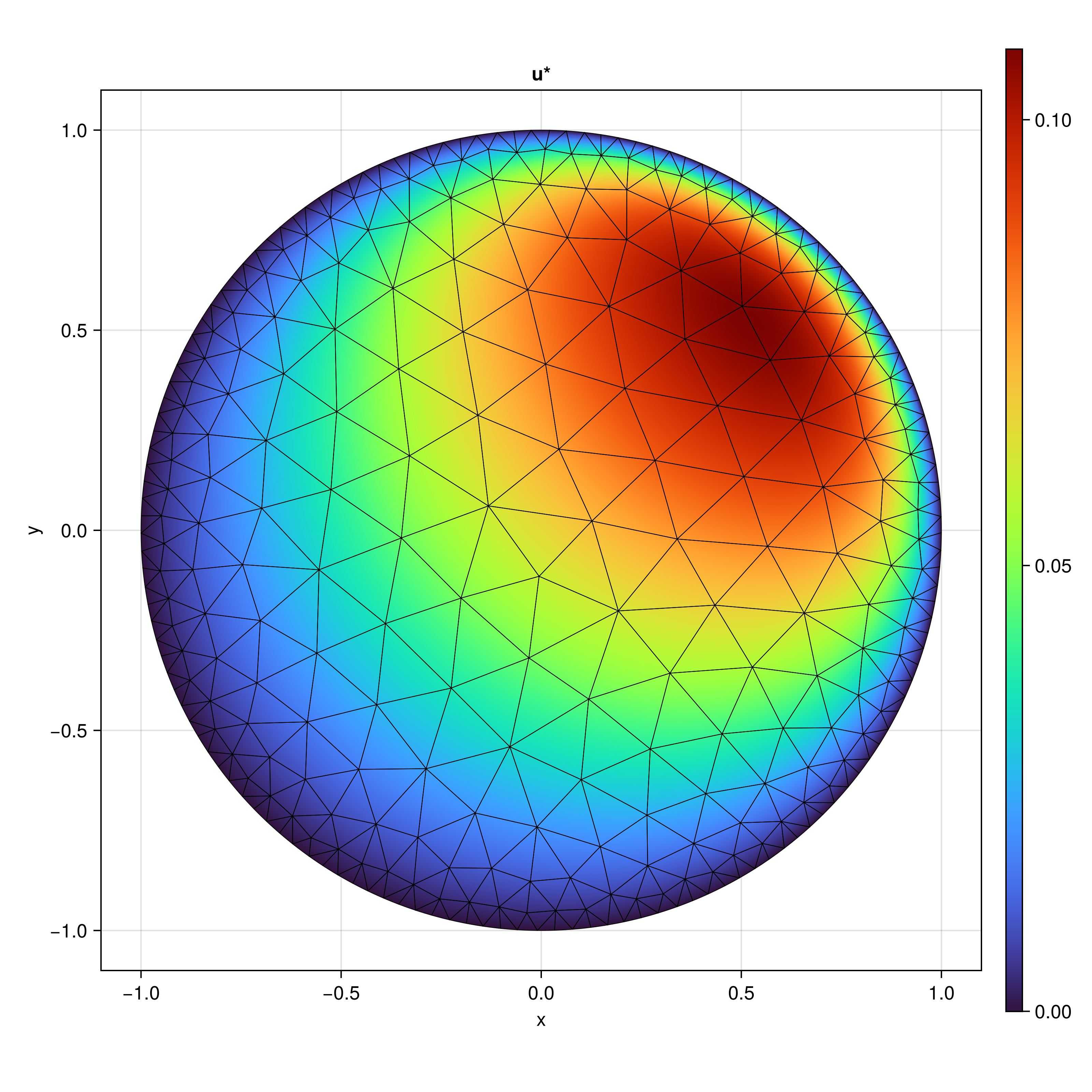Figure 3. Convection-diffusion solution in a circular domain on an unstructured triangular mesh (h=0.2) solved with Hybridizable Discontinuous Galerkin (HDG) at polynomial order p=4. The simulation shows a concentration field being transported diagonally with velocity (10,10) while diffusing with κ=1. HDG's static condensation dramatically reduces computational cost by solving only for trace variables on element edges, then recovering interior solutions in parallel.
What are Discontinuous Galerkin Methods?
The Challenge of Solving PDEs
Many phenomena in nature are governed by partial differential equations (PDEs)—equations that describe how quantities like temperature, pressure, or velocity change in space and time. For example, the heat equation tells us how temperature diffuses through a material, while the Navier-Stokes equations describe how fluids flow.
For most real-world problems, we cannot solve these equations analytically. Instead, we need numerical methods that approximate the solution numerically. The basic idea is to divide the spatial domain into small pieces (called elements or cells), represent the solution within each piece using simple functions (like polynomials), and enforce the equations in some averaged sense.
Traditional Finite Element Methods
The classical finite element method (Continuous Galerkin or CG) represents the solution using polynomials that are continuous across element boundaries. Imagine approximating a curve using straight line segments—the segments must connect smoothly at their endpoints. This works well for many problems, but it has limitations when dealing with discontinuities, like shock waves in fluids or sharp fronts in concentration fields.
The Discontinuous Galerkin Approach
Discontinuous Galerkin methods take a different approach: they allow the solution to be discontinuous at element boundaries. Think of it as using line segments that don’t necessarily connect smoothly—there can be jumps between elements. This might seem like a bad idea at first, but it comes with several powerful advantages:
- Shock capturing: DG methods can naturally represent sharp discontinuities like shock waves without oscillations (see Figure 1 for an example)
- Local conservation: Each element conserves mass, momentum, and energy independently
- Flexibility: You can easily use different polynomial orders in different regions
- Parallelization: Elements are weakly coupled, making the method naturally parallel
To connect the discontinuous solutions between elements, DG methods use numerical fluxes at interfaces—carefully designed functions that communicate information between neighboring elements while respecting the underlying physics.
High-Order Accuracy
One of the most attractive features of DG methods is that you can easily achieve high-order accuracy by using higher-degree polynomials within each element. While traditional methods might use straight lines (1st order) or parabolas (2nd order), DG methods routinely use 4th, 5th, or even higher-order polynomials. This means you can achieve very accurate solutions with relatively few elements, which is crucial for expensive simulations like turbulence or multiscale flows.
What is TwoDG.jl?
TwoDG.jl implements three complementary finite element discretization schemes in pure Julia:
- Continuous Galerkin (CG) - The traditional approach where solutions are continuous across elements
- Discontinuous Galerkin (DG) - High-order explicit time-stepping with discontinuous representations
- Hybridizable Discontinuous Galerkin (HDG) - An advanced variant that dramatically reduces computational cost through static condensation
What makes HDG particularly clever is its use of static condensation. Instead of solving for the solution everywhere simultaneously (which creates enormous systems of equations), HDG first solves only for values on element faces, then recovers the interior solution element-by-element in parallel. For high-order methods, this can reduce the system size by an order of magnitude while maintaining accuracy. It’s like solving a jigsaw puzzle by first figuring out the edge pieces, then filling in each interior section independently.
The framework handles diverse physics: Poisson equations, convection-diffusion transport, wave propagation with absorbing boundaries, and the full 2D compressible Euler equations with shock waves. All of these use the same underlying infrastructure—you just swap out the flux functions to change the physics.
Currently, TwoDG.jl supports solving equations in 2 spatial dimensions, with triangular elements on a structured and unstructured grid. There are some unstructured grids generator in this package with DistMesh, as well as Gmsh.
Compressible Flow Example (Figure 1)
Let’s look more closely at the channel flow simulation shown in Figure 1. This demonstrates the Discontinuous Galerkin method solving the 2D Euler equations:
∂ρ/∂t + ∇·(ρu) = 0
∂(ρu)/∂t + ∇·(ρu⊗u + pI) = 0
∂(ρE)/∂t + ∇·((ρE + p)u) = 0
These equations conserve mass (density ρ), momentum (ρu), and total energy (ρE) for a compressible gas. The simulation uses:
- Mesh: 16×8 elements with 5th-order polynomials
- Time integration: Explicit 4th-order Runge-Kutta with timestep Δt = 0.001 seconds
- Numerical flux: Roe approximate Riemann solver for shock capturing
- Physical parameters: Specific heat ratio γ = 1.4 (air), freestream Mach number M∞ = 0.3
The simulation runs for 4 seconds of physical time, capturing how shock waves form and propagate when the flow encounters the geometric perturbation. The method handles these discontinuities cleanly without spurious oscillations.
Convection-Diffusion Example (Figure 3)
The simulation shown in Figure 3 demonstrates the Hybridizable Discontinuous Galerkin (HDG) method solving a steady-state convection-diffusion equation on a circular domain. This represents a more challenging problem where both transport by flow (convection) and molecular spreading (diffusion) occur simultaneously.
The HDG method solves the equation -∇·(κ∇u) + c·∇u = f where the convection creates directional transport while diffusion smooths the solution:
- Mesh: Unstructured triangular mesh on a circular domain with element size h = 0.2 and refined boundary layers
- Method: Hybridizable Discontinuous Galerkin (HDG) with static condensation
- Polynomial order: p = 4 (quintic polynomials within each element)
- Physics:
- Diffusivity κ = 1
- Convection velocity c = (10, 10) (strong diagonal flow)
- Uniform source term f = 1
- Homogeneous Dirichlet boundary conditions (u = 0 on circle boundary)
The figure shows the post-processed solution u*, which achieves superconvergence through HDG’s local element-by-element enhancement procedure. Starting from the 4th-order accurate HDG solution, the post-processing recovers a solution with (p+2) = 6th-order accuracy at negligible additional cost. This is one of HDG’s key advantages—you get higher-order accuracy essentially for free through post-processing.
The strong diagonal convection (c = 10 in both directions) combined with unit diffusivity creates a convection-dominated problem (Péclet number ≈ 10), making this an excellent test of HDG’s ability to handle both physical phenomena while maintaining stability and accuracy on unstructured meshes.
Key Technical Features
Basis Functions: All methods use Koornwinder orthogonal polynomials on triangles, which are constructed from Jacobi polynomials. These provide optimal numerical conditioning and allow arbitrary polynomial orders (p-refinement).
Mesh Flexibility: Built-in generators for squares, circles, L-shapes, NACA airfoils, and ducts. Supports both straight and curved elements for representing complex geometries accurately.
Master Element Framework: The code precomputes shape functions, derivatives, and Gauss quadrature rules on a reference element, then maps them to physical elements. This separation of reference and physical spaces is fundamental to efficient finite element implementations.
Performance Optimization:
- Inline functions and array views minimize memory allocations
- Pre-factored mass matrices (using LU decomposition rather than inversion for stability)
- Thread-parallel assembly for HDG using
Threads.@threads - Careful pre-allocation of flux arrays
Time Integration: Explicit 4th-order Runge-Kutta for DG methods, allowing large stable timesteps while maintaining high accuracy.
Visualization: Integrated plotting with CairoMakie, including proper handling of curved elements and high-order solution fields.
What Can You Do With It?
- Compare different discretization methods on the same problem to understand their trade-offs
- Run convergence studies to verify that you’re achieving optimal error rates (typically p+1 for DG)
- Solve wave scattering problems with absorbing boundaries using the Trefftz method
- Simulate compressible flows including shock formation and wave propagation
- Analyze convection-diffusion transport with various stabilization strategies
- Develop new numerical methods using the extensible master element framework
Future Plans
As with most things in life, the ideas below are aspirational.
I wish I would be able to work on them, but all the time sometimes I get distracted by other things.
But if I want to run some ocean simulations on it, I better complete the final few pieces of the puzzles!
However, these ideas are, in principle, straightforward to extend.
Incompressible Navier-Stokes
Currently, the framework handles compressible Euler equations beautifully, but the real aspiration is to solve the full incompressible Navier-Stokes equations—the governing equations for flows where viscosity matters and density remains nearly constant (think ocean currents). This would enable simulation of turbulent flows, flow separation around bluff bodies, and realistic engineering applications.
Adding incompressible Navier-Stokes capability would require:
- Implementing pressure-velocity coupling schemes
- Nonlinear solvers for the convective term (u·∇u)
This would open up applications in fluid-structure interaction, ocean modeling, biological flows, and turbulence simulation.
Extension to 3D
While the current implementation focuses on 2D problems, the mathematical framework naturally extends to three dimensions. The main development efforts would involve:
- Extending the master element framework to tetrahedral elements
- Implementing 3D mesh generators and handling curved 3D elements
- Optimizing memory access patterns for 3D arrays (where cache efficiency becomes even more critical)
Three-dimensional simulations would enable realistic engineering applications like flow around aircraft wings, acoustic scattering from complex 3D objects, and turbulent flows in pipes or channels.
Nonlinear Problem Support
While the current framework excels at linear problems and handles the nonlinear Euler equations, comprehensive support for more nonlinear problems would require:
- Implicit time integration schemes (Backward Euler, BDF methods) for stiff problems
- Newton-Raphson solvers for systems of equations with Jacobian assembly
- Jacobian-Free Newton-Krylov (JFNK) methods for large-scale problems
- Nonlinear HDG formulations with Newton iterations for the condensed system
Currently, the HDG implementation solves linear problems using static condensation and direct sparse solves. Extending HDG to nonlinear problems would involve iteratively updating the condensed system matrix and residual within Newton loops, while preserving the efficiency gains from static condensation. This would be particularly powerful for nonlinear diffusion problems, p-Laplacian equations, and the nonlinear convective terms in Navier-Stokes.
This infrastructure would enable steady-state nonlinear problems (like Burgers’ equation), implicit shock capturing, and nonlinear diffusion problems, and of course incompressible Navier-Stokes, where the convective term u·∇u creates strong nonlinearity.
GPU Acceleration
Julia’s GPU ecosystem (CUDA.jl, AMDGPU.jl, KernelAbstractions.jl) makes it natural to port high-performance numerical codes to GPUs. For DG methods, GPUs are particularly attractive because:
- Element-local operations (flux computations, local mass matrix inversions) are embarrassingly parallel
- The discontinuous nature means minimal communication between elements
- High arithmetic intensity makes good use of GPU compute capabilities
GPU acceleration could provide 10-100× speedups for large-scale problems, making previously intractable simulations feasible. The modular architecture of TwoDG.jl is designed with this in mind—most compute-intensive kernels are already separated into functions that could be dispatched to GPU kernels using KernelAbstractions.jl.
Combining these directions (incompressible Navier-Stokes + nonlinear solvers + 3D + GPU) would create a truly powerful framework capable of tackling industrial-scale CFD problems while maintaining the clarity and flexibility that makes it excellent for research and education.
Code and Resources
The code is available on Github:
Feel free to explore the code, run the examples, and adapt it for your own problems. The modular structure makes it straightforward to add new physics or boundary conditions while reusing the robust infrastructure for assembly, solving, and visualization.
Of course, this project would never have been possible with the help of Professor Jaime Peraire, who was incredibly generous with his time to help me debug through many issues, and wholeheartedly rooted for the success of this effort through and through.